Introdução

Nesse artigo, será apresentado uma pequena explicação a respeito da Lei de Benford, formas de cálculo, uso, aplicações e forma de verificar a aderência a lei. Ao final, uma aplicação prática usando a base de demonstração do Microsoft Contoso BI para o setor de varejo.

1. Contexto Histórico

A Lei de Benford, também conhecida como a Lei do Primeiro Dígito, foi observada pela primeira vez em 1881 pelo astrônomo americano Simon Newcomb. Ao analisar tabelas de logaritmos, Newcomb notou que os primeiros dígitos dos números tendiam a seguir uma distribuição específica: o dígito 1 aparecia com muito mais frequência do que o esperado.

Em 1938, o físico americano Frank Benford redescobriu e popularizou essa lei ao testá-la em diversos conjuntos de dados, como números de casas, populações e constantes físicas. Seus resultados confirmaram a observação de Newcomb, mostrando que a distribuição dos primeiros dígitos não era uniforme, mas sim seguia um padrão logarítmico.

2.Conceitos

A Lei de Benford estabelece que, em muitos conjuntos de dados numéricos do mundo real, a probabilidade de um dígito inicial ser "d" (onde d pode ser 1, 2, ..., 9) é dada por:

P(d) = log10(1 + 1/d)

Essa fórmula implica que o dígito 1 aparece como primeiro dígito em aproximadamente 30% dos casos, o dígito 2 em cerca de 17,6%, e assim por diante, com a probabilidade diminuindo à medida que o dígito aumenta.

3. Como Usar

Para aplicar a Lei de Benford, é necessário: 1. Coletar um conjunto de dados numéricos relevantes para a análise. 2. Identificar o primeiro dígito de cada número no conjunto de dados. 3. Calcular a frequência de cada dígito inicial. 4. Comparar as frequências observadas com as frequências esperadas de acordo com a Lei de Benford.

4. Onde Pode Ser Usada

A Lei de Benford pode ser aplicada em diversas áreas, como: - Ciências: Análise de dados experimentais, como medições físicas e químicas. - Auditoria: Detecção de fraudes em dados contábeis e financeiros. - Finanças: Avaliação de risco em carteiras de investimento e análise de dados de mercado. - Estatística: Verificação da qualidade de dados e identificação de outliers.

5. Onde Não Pode Ser Usada

A Lei de Benford não se aplica a todos os conjuntos de dados. Ela é mais adequada para dados que: - São gerados por processos naturais ou sociais complexos. - Abrangem uma ampla gama de magnitudes. - Não são influenciados por fatores externos que possam distorcer a distribuição dos dígitos.

6. Aplicações Práticas

A Lei de Benford tem sido utilizada em diversas aplicações práticas, como: - Detecção de fraudes contábeis: Desvios significativos da distribuição esperada podem indicar manipulação de dados. - Análise de eleições: Verificação da integridade dos resultados eleitorais. - Avaliação de risco de crédito: Identificação de padrões de comportamento em dados de crédito.

7. Margens de Erro

A Lei de Benford não é uma ferramenta infalível. Desvios da distribuição esperada podem ocorrer devido a fatores legítimos, como características específicas dos dados ou erros de medição. A determinação de margens de erro aceitáveis depende do contexto e da área de aplicação.

8. Introdução do Teste Qui-Quadrado (χ²)

O teste qui-quadrado (χ²) é um teste estatístico utilizado para comparar as frequências observadas de um conjunto de dados com as frequências esperadas de acordo com uma distribuição teórica, como a Lei de Benford. Ele quantifica a discrepância entre as frequências observadas e esperadas, permitindo avaliar se essa discrepância é estatisticamente significativa.

9. Motivo de Uso do Teste Qui-Quadrado

O teste qui-quadrado é utilizado em conjunto com a Lei de Benford para: - Avaliar a aderência dos dados à lei: Verificar se a distribuição dos primeiros dígitos observada é consistente com a distribuição esperada pela Lei de Benford. - Quantificar a significância estatística de desvios: Determinar se desvios da distribuição esperada são provavelmente devidos ao acaso ou indicam uma possível manipulação de dados.

10. Aplicação Prática

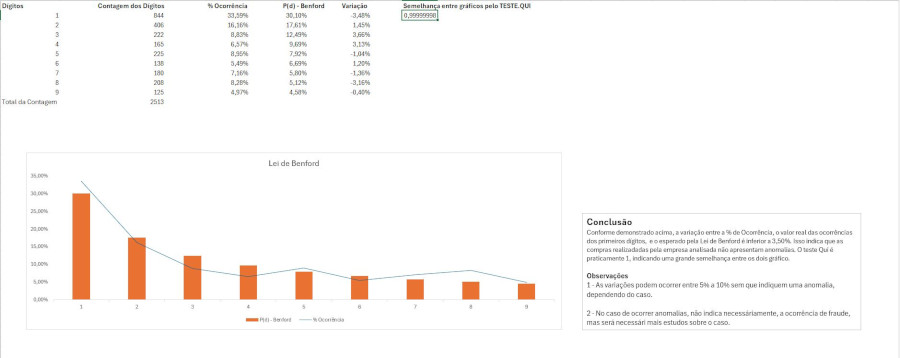
Foi aplicado a Lei de Benford do conjunto de dados de demonstração do Microsoft Contoso BI para o setor de varejo. A tabela usada foi a DimProduct no qual possui os preços dos 2518 produtos comercializados. Os dados foram importados do banco SQL para o Excel. A base foi tratada no Power Query, no qual foram removidas as colunas desnecessárias. Após isso, foi feito a "implementação" da Lei de Benford no Excel. Verificou-se que a do P(d) foi de -3,48 a 3,66 pontos percentuais. Para avaliar melhor a similaridade do resultado, foi usado teste qui-quadrado, resultando em um valor de 0,99999998. Vale lembrar que, quanto mais próximo de 1 for o resultado, maior a similaridade entre as curvas.